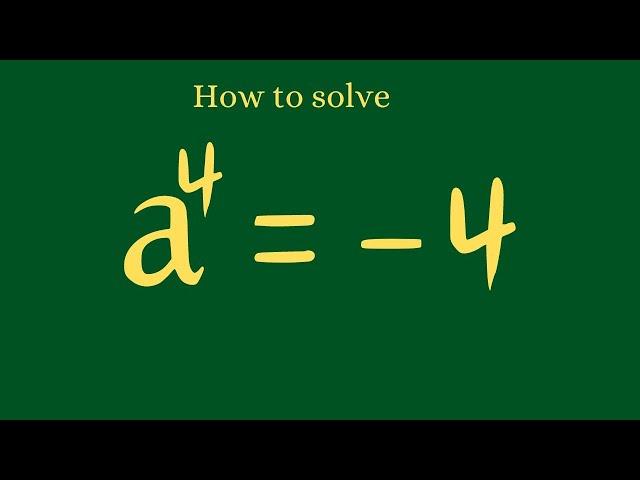
Russia Math Olympiad | How To Solve For All 4 Imaginary Roots In This Nice Exponential Equation.

Thanks so much for this expository clip. Greater heights sir.🎉

Thank you very much my dear friend

Thanks

Классика жанра:
Четвертая степень => четыре корня!

,(√2√i)^4=-4

Thanks

Enjoyable tutorial, I was able to follow and understand every step. I just LOVE ALGEBRA! It is such a relaxing pastime for me!

Thank you very much my dear friend

knesolvh tebedda kalbeqahtebedadadadadadas...

a = e^(0.25ln(4) + 0.25ipi + 0.5ipin), n is a integer

Great!!

Clear explanation thanks

ممتع ،، من العراق

Method 2?

a=a or a=/a ???!!!

Thank you .good luck

really need this comp?

Great

Nice video

-1 = a

عمال الوكالة الرابعة بن طلحة ومالحقة المديرية العامة بالمحمدية وكذا خلية الأمن الداخلي إضافة داءرة الصيانة وكذا مصالح داءرة المحاسبة تورطو في اتلاف مقررات عدالة وقراري ترقية وكذا الإعداد لحوادث مع فرقة الصيانة ببن طلحة وحي الفين واربعة مسكن وحوش ميهوب عن طريق عناصر تمنية متخفية تشغل مناصب في الديوان كما اعدو لحوادث خطيرة كالحراءق المنزلية مع مؤسسات كالداءرة و البلدية بتواطؤ مصالح الأمن شرطة جيش ودرك وامن بمساندة دول اجنبية كتركيا وفرنسا وانجلترا واوكد الدور الذي لعبتهمضباط واطارات امنية حضرت ابن طلحة لاعطاء إشارات ان الدولة سترعى المجرمين ضد الشاب اوباغة طاهر كما أذكر دور سكان الاحياء كي الف وثمتنية وسبعين مسكن في فبركة الحوادث و القيام بالضغط بتواطؤ عمال الوكالة

Nice approach master

- a

Le faltó comprobar que a^4=-4. Cualquier profesor de matemáticas sabe que hay que comprobar las soluciones con el único propósito de verificar que la respuesta sea cierta

Easy

Theorem. The solutions of the equation xⁿ=a, where a is a negative real number, are
xᵢ = ⁿ√∣a∣ ⋅ ԑᵢ (i = 0, 1, ..., n - 1),
where ԑᵢ are the nth roots of -1.

fine! Thank you!

a^4 > or =0 => a^4= -4 wrong 😤

a=(1+i)^4 0r a=(1-i)^4

я из росии, но подача мне понятна

Put isquare is -1 then it will be 2i , think, what about u

لماذا كل هذه الزوبعة ، كان يمكن الحصول على الحل بطريقة بسيطة جدا فور الاطلاع على المعادلة.

Why did I get different complex roots? I got sqrt(2i), -sqrt(2i), sqrt(-2i) and -sqrt(-2i). When you plug these roots in the equation it is true. Could someone explain?

Меня восхищает, когда квадратное уравнение a² + 2a + 2 = 0 решается с помощью формулы для корней. Это же гениально. А если переписать это в виде (a + 1)² = -1; не станет ли это проще, понятнее и ну как-то ... разумнее, что-ли?
Надо сказать, что я когда-то "сел" (опростоволосился) на первом курсе. Нужно было взять интеграл от 1/(x⁴ + 1), а я не догадался, что знаменатель раскладывается в произведение двух многочленов второй степени. Справедливости ради стоит сказать, что до того момента я никогда не слыхал об основной теореме алгебры. На самом деле любой многочлен четвертой степени с действительными коэффициентами может быть разложен таким образом, так как комплексные корни могут существовать только парами сопряженных. В точности как в этой задачке. Детям сейчас это рассказывают, а вот нам не рассказывали, от слова совсем.

I was trying to do it directly by stating the difference of two squares using i. (a^2+2i)(a^2-2i)=0
But now I end up needing to square root the imaginary, meaning I would have to set it up to a+bi. Your creative way turns out simpler, although that too had a lot of steps

i hate the man who makes question. 🤣
but my man can solve this question easly

Sorry but you're rong

This is to long

Nice work my brother.
Keep it up

Понравилось.

もっと簡単にできる方法はないか

Very nice

Very nice process of derivation by applying a few very useful techniques. My approach is just doing this. a^4 -> (a^2)^2, -4 -> (2i)^2 and -4 -> ((-2)*i)^2, so a1^2 = +/-sqrt(2i) and a2^2 = +/-sqrt(-2i). 2i -> (1+i)^2 and -2i -> (1-i)^2, so a1=+/-(1+i) and a2=+/-(1-i). Therefore the final solution is a1=1+i, a2=1-i,a3=-1+i, and a4=-1-i.

Here is another way to solve this equation and I believe this might be little easier

1. a^4 = -4
2. (a^2)^2 = 2^2 * (-1) (Case A) or (-a^2)^2 = 2^2 * (-1) (case B)
3. Let us solve Case A first, where (a^2)^2 = 2^2 * (-1)
4. Taking square root of both side a^2 = 2i
5. Taking square root of both side a = ✓2*✓i
6. Square root of i = 1/✓2 + i/✓2 and –(1/✓2 + i/✓2)
7. So a = ✓2*(1/✓2 + i/✓2) and a= ✓2*-(1/✓2 + i/✓2)
8. So a = (1+i) or a = -(1+i)
9. Now take the Case B, where (-a^2)^2 = 2^2 * (-1)
10. (-a^2)^2 = 2^2 * (-1)
11. Taking square root of both side -a^2 = 2i
12. a^2*i^2 = 2i
13. Taking square root of both side a * i = ✓2*✓i
14. Or a = ✓2/✓i
15. Square root of i = 1/✓2 + i/✓2 and –(1/✓2 + i/✓2)
16. So a = ✓2/(1/✓2 + i/✓2) and a = ✓2/-(1/✓2 + i/✓2)
17. So a = (1-i) or a =-(1-i)
18. Four values of a = (1+i) or a = -(1+i) or a = (1-i) or a =-(1-i)

Thanks 👍

Dear,

Warm greetings from Bohnsdorf, Germany. I wanted to take a moment to express my sincere appreciation for the incredibly informative video you recently posted. Your content is not only highly engaging but also remarkably clear and understandable.

I've taken the liberty to subscribe to your channel, and I eagerly anticipate the release of your future videos. Your dedication to providing valuable content does not go unnoticed, and I'm grateful to be part of your audience.

Thank you once again for your efforts in creating such enriching content.

Best regards

Простое уравнение. Решение очевидно.

👍👍👍

Hay un error en el enunciado porque ésto parte de un error ,de acuerdo a la teoría de exponentes todo número elevado a un exponente par ya sea el número positivo o negativo ,siempre se tendrá como resultado un número positivo

Решаем уравнение, а^4=4, а затем находим корни на окружности с радиусом корень(2).