Комментарии:

a = 7; b = 5.
Ответить
👍
Ответить
a² - b² = 24
ab = 35
a² + (-b²) = 24
a²(-b²) = -1225
t² - 24t - 1225 = 0 [ a² and -b² are the roots ]
t = 12 ± 37 => t = 49 ∨ t = -25
t = 49 => a = ± 7
a = 7 => b = 5
a = -7 => b = -5
t = -25 => a = ± 5i
a = 5i => b = -7i
a = -5i => b = 7i

Why do not square ab=35 first, without x-y substitution?
a²b²=1225
a²(-b²)=-1225
a²+(-b²)=24
Due to Vieta's formula a² and -b² are the solution of the quadratic equation
t²-24t-1225=0
t=-25, t=49
etc.

7. 5
Ответить
a² - b² = 24
ab = 35
a² - b² = 24 ==> a² = b² + 24
ab = 35 ==>
a²b² = 35²
(b² + 24)*b² = 35²
(b²)² + 24b² = 35²
(b²)² + 2*12b² + 144 = 35² + 144
(b² + 12)² = 35² + (35 + 36) + (36 + 37) = 37²
(b² + 12) = ±37
b² = -12 ± 37
b² = 25 OR b² = -49
b = ±5 OR b = ±7i
a = 35/b ==>
(a, b) = (±7 , ±5) OR (a, b) = (±5i , ∓7i)

You can using complex analysis method to solving it sir.
Ответить
At my first sight i looked in ab and thought whats the answer would be only finding the factors of 35.and i found all the real solutions from the factor
Ответить
(a^2 - b^2)^2 = a^4 - 2(ab)^2 + b^4 = 24^2 = 576, (ab)^2 = 35^2 = 1225. Add 4(ab)^2 = 4900 to both sides: a^4 + 2(ab)^2 + b^4 = 5476 --> (a^2 + b^2)^2 = 5476 = 74^2.
From this a^2 + b^2 = +74 or a^2 + b^2 = -74. We can add the 1st given equation to both to give us: 2a^2 = 98 or 2a^2 = -50. From this a^2 = 49 and a^2 = -25 follow.
This gives us a = 7, a = -7, a = 5i and a = -5i. Now we use the second given equation of ab = 35 to find b. b = 35/a. This gives us b = 35/7 = 5, b = 35/-7 = -5, b = 35/5i = -7i and b = 35/-5i = 7i.
So (a,b) = {(7,5), (-7,-5), (5i,-7i), (-5i,7i)}.

"remember, recently, we told about i". 😂
Yes, I think that's why this channel is called aplusbi 😂

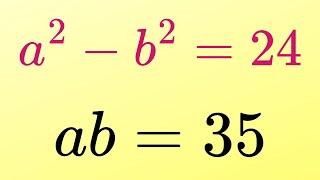







![Underverse OST - GENOCIDE [Genocide X!Frisk's Theme] Underverse OST - GENOCIDE [Genocide X!Frisk's Theme]](https://invideo.cc/img/upload/SXMyQ1VvRlgtNFk.jpg)

















