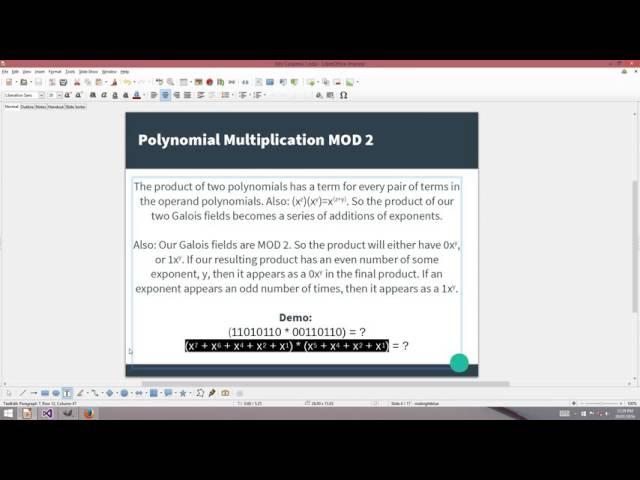
Комментарии:

This is really good! Thank you!
Ответить
This awesome ! please continue. awaiting the next video. gday mate.
Ответить
Very informative. Looking forward to the Matrix Multiplication video.
Ответить
Thank you so much.
This content is so great!!!!

i think the quickest way is to shift left if byte begins with 0, else if it begins with 1, shift left and XOR with 27 (00011011)
Ответить
AMAZING EXPLAINATION....
Ответить
thank you very much! a perfect explanation!
Ответить
well done, i'm really grateful thanks much more than a lot
Ответить
Hello,
the videos were of real help but i am finding difficulty in executing it. Could you send me the source code so that i could see where have i got wrong! My mail ID : [email protected] . thanks in advance. :)

Could you make the file available?
Ответить
great video, but isnt it x^4+1 modulus rather than x^8+x^4+x^3+x+1?
Ответить
Sweet Jesus.
Ответить
please teach me about calculator invmixcolumns ?
Ответить
What's a Creel Can you make RSA Encryption tutorial Please ? <3
Your video are fantastics

u r really too good
Ответить
Thank you for making this video. Learned a bunch from you :)
Ответить
Thank you so much!. Your videos helped me a lot to finish my 8th semester thesis. I don't know your name so I putted your channel in the reference page :).
Ответить
Mult3 table is useless. Use Mult3(x)=Mult2(x)xor(x).
Also Mult2 is a bit overkill. In polynomial perspective ×2 is ×(x) so it's left shift then you have to reduce. But only if top bit was 1. In that case you just have to replace x^8 by the reminder of x^8 / (x^8+x^4+x^3+x^1+1) and adding that to the lower bits is adding x^4+x^3+x^1+1 ie xoring with 0x1b

Awwww. You make this look so easy but the worst part about this is whole AES thing is having to do the InvMixColumns
Ответить
Hi! I was going through your video and I think they are really helpful. The lookup tables for mul2 and mul3 are not available on Wikipedia and I can’t seem to find them on the internet... I know this is a long shot but do you still happen to have them?
Ответить
i can't find out multiply by 2 lookup table in hex format?
can you send me link?

The best AES explanation forever. Thanks a lot!
Ответить
You saved my life, thank youuu 😍
Ответить
Lookup-tables are not available anymore. I wrote down the one shown in this video:
0x00, 0x02, 0x04, 0x06, 0x08, 0x0a, 0x0c, 0x0e, 0x10, 0x12, 0x14, 0x16, 0x18, 0x1a, 0x1c, 0x1e,
0x20, 0x22, 0x24, 0x26, 0x28, 0x2a, 0x2c, 0x2e, 0x30, 0x32, 0x34, 0x36, 0x38, 0x3a, 0x3c, 0x3e,
0x40, 0x42, 0x44, 0x46, 0x48, 0x4a, 0x4c, 0x4e, 0x50, 0x52, 0x54, 0x56, 0x58, 0x5a, 0x5c, 0x5e,
0x60, 0x62, 0x64, 0x66, 0x68, 0x6a, 0x6c, 0x6e, 0x70, 0x72, 0x74, 0x76, 0x78, 0x7a, 0x7c, 0x7e,
0x80, 0x82, 0x84, 0x86, 0x88, 0x8a, 0x8c, 0x8e, 0x90, 0x92, 0x94, 0x96, 0x98, 0x9a, 0x9c, 0x9e,
0xa0, 0xa2, 0xa4, 0xa6, 0xa8, 0xaa, 0xac, 0xae, 0xb0, 0xb2, 0xb4, 0xb6, 0xb8, 0xba, 0xbc, 0xbe,
0xc0, 0xc2, 0xc4, 0xc6, 0xc8, 0xca, 0xcc, 0xce, 0xd0, 0xd2, 0xd4, 0xd6, 0xd8, 0xda, 0xdc, 0xde,
0xe0, 0xe2, 0xe4, 0xe6, 0xe8, 0xea, 0xec, 0xee, 0xf0, 0xf2, 0xf4, 0xf6, 0xf8, 0xfa, 0xfc, 0xfe,
0x1b, 0x19, 0x1f, 0x1d, 0x13, 0x11, 0x17, 0x15, 0x0b, 0x09, 0x0f, 0x0d, 0x03, 0x01, 0x07, 0x05,
0x3b, 0x39, 0x3f, 0x3d, 0x33, 0x31, 0x37, 0x35, 0x2b, 0x29, 0x2f, 0x2d, 0x23, 0x21, 0x27, 0x25,
0x5b, 0x59, 0x5f, 0x5d, 0x53, 0x51, 0x57, 0x55, 0x4b, 0x49, 0x4f, 0x4d, 0x43, 0x41, 0x47, 0x45,
0x7b, 0x79, 0x7f, 0x7d, 0x73, 0x71, 0x77, 0x75, 0x6b, 0x69, 0x6f, 0x6d, 0x63, 0x61, 0x67, 0x65,
0x9b, 0x99, 0x9f, 0x9d, 0x93, 0x91, 0x97, 0x95, 0x8b, 0x89, 0x8f, 0x8d, 0x83, 0x81, 0x87, 0x85,
0xbb, 0xb9, 0xbf, 0xbd, 0xb3, 0xb1, 0xb7, 0xb5, 0xab, 0xa9, 0xaf, 0xad, 0xa3, 0xa1, 0xa7, 0xa5,
0xdb, 0xd9, 0xdf, 0xdd, 0xd3, 0xd1, 0xd7, 0xd5, 0xcb, 0xc9, 0xcf, 0xcd, 0xc3, 0xc1, 0xc7, 0xc5,
0xfb, 0xf9, 0xff, 0xfd, 0xf3, 0xf1, 0xf7, 0xf5, 0xeb, 0xe9, 0xef, 0xed, 0xe3, 0xe1, 0xe7, 0xe5,

Is there some sort of a "test suite" with an example message, its ciphertext, and all the intermediate states, so that one could verify if one's implementation works correctly and produces the same ciphertexts as other implementations? This is very important, because if the algorithm is implemented in a wrong way, it would still produce some gibberish that would look like encryption, and chances are that its inverse would be able to restore the original message from that gibberish, but it will be incompatible with other implementations and unable to decrypt messages encrypted with those other implementations correctly. So how can one verify if the implementation is doing the right thing?
Ответить
Finally a video on actual solving of "MixColumns in AES" !! So thankful.Bless you :)
Ответить
damn this was helpful! thank you !
Ответить
thanku!!!!!
Ответить
This is honnestly the best explanation i seen, thanks!
Ответить
This video is just magnificent. Well done dude!
Ответить
thx sir
Ответить
good stuff
Ответить
For mul3, couldn’t you just mul2(a) xor a? Why store an extra 256 bytes? Is the latency from the xor noticeable?
Ответить
I need code matlab
For aes
Please

Great video. This is the one place where I was actually able to get code to perform the MixColumns operation. That one extra step where you have to deal with the most significant bit being set seemed to make all of the difference. Thanks for the video and thanks for the code!
Ответить
FINALLY, someone who can explain this clearly…..thank you!!
Ответить