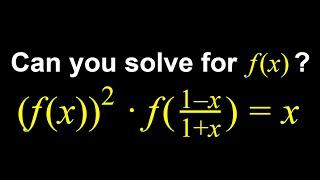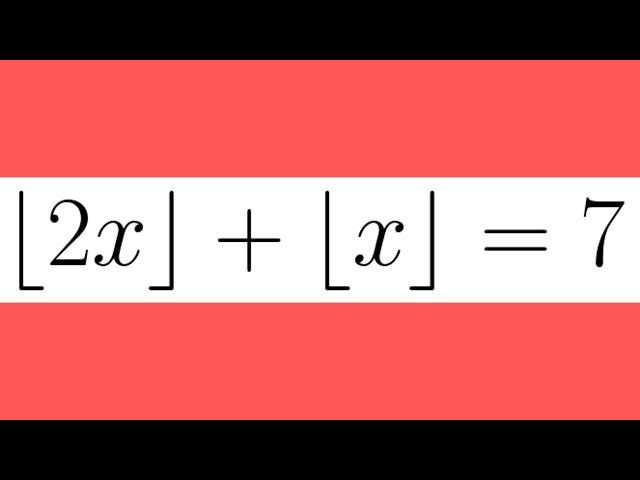
An equation with floor values! An algebraic adventure in equations and inequalities...

3x=7
x=7/3

solve
floor (x) +ceuk(x) = x*2

Thank you

Amazing work, can you make a video about answer of x_[x/4]>0
X minus floor of x over 4 when is greater than zero

👍

The floor function is non-decreasing, and the left-hand expression always increases at integer and half-integer x. So it's enough to observe x=2.5 is a solution.

what about the intervalle [7/3;3[

Not too difficult. We just be careful about the floors. I'll use [x] for the floor. [x] = n. n ≤ x < n + 1. 2n ≤ 2x < 2n + 2. So [2x] = 2n or 2n+1. 2n + n = 7 doesn' work, but 2n+1 + n = 7 does. n = 2, and [2x] = 2n+1. So 2.5 ≤ x < 3.

Case I : n <= x < n + 1/2
i.e 2n <= 2x < 2n +1
This implies 3n = 7 resulting in no feasible solution .

Case I : n +1/2 <= x < n +1
i.e 2n +1 <= 2x < 2(n +1 )
This implies 3n +1 = 7 resulting in
n = 2
So 2 +1/2 <= x < 2 +1
Only feasible solution .

What about "1-floor(x)+ceil(x)", a kind of infinite pulse queue? Can it be integrated from 0 to Infinity? What is the result? 1.0?

Is it wrong to add both inequalities n <= x < n+1 and 7-n <= 2x < 8-n to get 7 <= 3x < 9 ? Which let us know that x must be slightly greater than 2 but less than 3, hence n = 2, and then we proceed to find floor(2x) = 5

compi finds the interval too:
Reduce[Floor[2 x] + Floor[x] == 7, x, Reals]

There is another way to solve it
Let's write x as n+q, where n=[x] and q={x}
Then basical equation is tantamount to 3n+[2q]=7, and we can notice that 0≤2q<2, what means that [2q] is 0 or 1. 3n is divisible by 3 => 7-[2q] is the same => [2q]=1 => n=2 and 1≤2q<2 => n=2 and ½≤q<1 => 2½≤x<3

👍

Good

A bit of trial and error can massively simplify these types of floor problems. Try x=2, this gives 6. Try x=3, this gives 9. So we know 2<x<3. But then floor(x)=2, and so the equation simplifies to floor(2x)=7-2=5. So, 5<=2x<6, or 5/2<=x<3. And we’re done. PS I love this channel, keep them coming!

Thanks. Very clear explanation.

I find this simpler: Put x = n + y, 0 <= y < 1. Then, 2x = 2n + 2y. Hence, floor(2x) = 2n if 0 <= y < 1/2 and = 2n + 1 if 1/2 <= y < 1. The first gives 3n = 7, no solutions, the second gives 3n + 1 = 7, n = 2. Hence, 2+1/2 <= x <= 2+1.

Maybe solve this: floor(2*x) = 2 * floor(x)

Thank you for the solution. I solved the problem this way: x=n+a, 0<=a<1, then 2x=2n+2a then [2x]=2n+[2a], where [2a]=0 if 0<=a<.5 and [2a]=1 if .5<=a<1. We need to consider both cases, the first one gives n=7/3 which is not an integer and the second one leads to 3n+1=7 then x=2+a where .5<=a<1.

nice solution sir thank u

Great job! Keep on going!