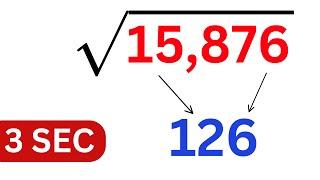
Square Root in 3 seconds - Crazy Math Trick

58

Can you make more videos that teaches tricks like this

and if the last number is 7 or 2?

How could crack like jee exams

3364:- 2/8 and 5 then 58

the method 0²=*0* 1²=*1* 2²=*4* 3²=*9* 4²=1*6* 5²=2*5* 6²=3*6* 7²=4*9* 8²=*64* 9²=8*1*

Which app do you use to edit your videos?

I may do this ib my calculator 😂

What a waste of time.....

Fun fact
81x196=15876

nice trick broo

start with 60^2 = 3600 then minus 60, 59, 59 58 to get to 3364. So answer is 58

Nice. But I'm afraid only useful in quizzes.

Sqrt[9]

That's because Jesse is at home, you're not. Time and feel again?

lol i calculated the first one in 5 seconds before watching the video

58

Thumbs down for using a robot voice.

Trick without an explanation is just a trick

didn't work for 998,001, at least not for me

John 14:6
New King James Version
6 Jesus said to him, “I am the way, the truth, and the life. No one comes to the Father except through Me.

appreciated 🔥

sqrt(3364) = 58.

I'll just keep using the sqrt function on my calculator

Noice

How do we pick, choose the first number or the second number?

58

58²=3,364

(a+b)²=a²+2ab+b²
(50+8)(50+8)
2,500+2(400)+64
2,500+800+64
3,300+64=3,364

(a-b)²=a²-2ab+b²
(60-2)(60-2)
3,600-2(120)+4
3,600-240+4
3,360+4=3,364

disliked it wasn't 3 seconds

Also works for cuberoot

I can just get a calculator and get the answer in less time than this video

58

Another quick way to find the correct answer between two choices is to cast out nines. For example, if the square root of 729 is either 23 or 27, we can first check 23 as a root by adding the digits together. 2+3 is 5, which gives us a remainder of 5. 23x23 gives us two remainders of 5, and we multiply them to get 25. 2+5=7. The nines remainder of 729 must also be 7, or we have the wrong root.
7+2+9=18, 1+8=9, and we can cast out the 9, giving us a remainder of zero. Seven does not equal zero, so 23 is not the correct root, and that leaves 27 as the only possible answer.

whats the thing/rule that allows this trick to actually work?

Skibidi

does this work for all perfect squares?

3364=4mod8
=(2mod8)x(2mod8)
33>5^2
64=8×8=4mod8
58=2mod8

It's a nice trick, but one small quibble. You started off saying you only need to learn the squares of 0 through 9, and you end by casually throwing in the square of 12.

misleading ... the trick allows you to quickly recognize a perfect square. it would take a normal person more like 30 seconds to apply the trick

What If It ends in 2,3,7 or 8?
Just go for the closer one? Higher one or lower one?

So good, keep going 👏 💪

ask a German if they know what the square root of 81 is, if they know, you get the correct answer, if they don’t know, you also get the correct answer

Why this works ig:
first, looking at the ones digit and getting the number whose square has the same ones digit obviously will give the ones digit.
To understand the entire method clearly,
here's what happens to a number when it's squared:
2 4
x 2 4
-------------
0 9 6
+4 8 0
--------------
5 7 6

Explaining the middle digit canceling: Middle digit is ignored in the process because it doesn't tell much about the number that was squared. The number that was squared had less digits than the result number, and that difference is these middle numbers that went bye bye. Also, 4 digit and 3 digit perfect squares both have 2 digit roots. if x is a tens digit and y is a ones digit, (10x+y)^2 is 100x^2+2xy+y^2. 2 of the numbers from 1 to 9 can multiply with each other up to 81 and 3 of them go up to 729.

why you need to find the square number just under the first digit:
Getting the square because during the multiplication process for squaring, the first digits of each number, which are the same number, are multiplied/"squared." Ex: the 2 in 24 multiplies with the 2 in 24. Thus, finding the squared number just below it or equal to it gets the first digit(s) of the square root. The first digit(s) being over the number squared is just an effect of carry over.

Why do you need to multiply with the next number and compare:

it has to do with if the one's digit passes or doesn't pass 5.
If we look at x5*x5 (x being the digit), then the method to get the 1st digit of the number (multiplied to 100) would be
10x*5+10x*5+10x*10x

which is 100x(1+x)
thus, the first digit x is compared to x(1+x)

as for how I got the expression above, I looked at the column method for a number ending in 5.
example for 24*24: to get the first component that will add to the first number, do 20*4. I skip the ones place because ones place digits can only yield up to the ten's place (carry over).
To get the 2nd component, do 20*4+20*20. In the column method, this corresponds to doing 2*4 with the 4 at the top right and 2*2 with the 2s in the same column, and then placing the digits below the first number.
add them up and u get a number with the same hundred's place as 576.
Replacing all the 20 with 10x and the 4 with 5 will get the formula thingy I used.


Why did I do this? idk
did it take me forever? yes
Was it fun? ykw sure