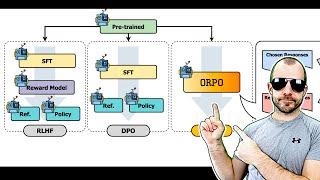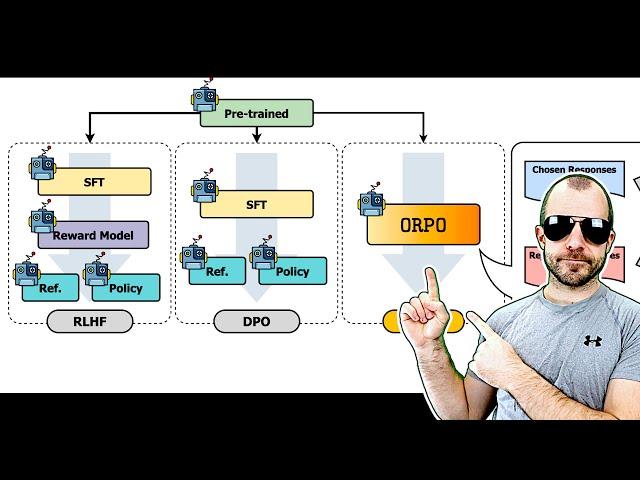
ORPO: Monolithic Preference Optimization without Reference Model (Paper Explained)

"Specifically, 1 - p(y|x) in the denominators amplifies the gradients when the corresponding side of the likelihood p(y|x) is low". I think that (1 - p(y|x)) have two different meanings here: it can be the result of differentiation by coincidence and also the "corresponding side" of the likelihood, i.e., 1 - p(y|x). So, when it says the "corresponding side" of p(y|x) is low, it means that 1 - p(y|x) is low.

Keep them comin

I found this more endearing than netflix 🥹❤️.

makes me think of PPO

What's going on, is it a yannic bonanza time of the year! Loving these addicting videos

The main loss function (7) looks like it can be meaningfully simplified with school-level math.

Recall that loss function (7) is
Lor = -log(sigm( log ( odds(y_w|x) / odds(y_l|x)))), where sigm(a) = 1/(1 + exp(-a)) = exp(a) / (1 + exp(a))
Let's assume that both odds(y_w|x) and odds(y_l|x) are positive (because softmax)

Then, plugging in sigmoid, you get
Lor = - log (exp(log(odds(y_w|x) / odds(y_l|x) )) / (1 + exp(log(odds(y_w|x) / odds(y_l|x)))) )
Note that exp(log(odds(y_w|x) / odds(y_l|x)) = odds(y_w|x) / odds(y_l|x). We use this to simplify:
Lor = - log( [odds(y_w|x) / odds(y_l|x)] / (1 + odds(y_w|x) / odds(y_l|x)) )
Finally, multiply both numerator and denominator by odds(y_l|x) to get

Lor = - log(odds(y_w|x) / (odds(y_w|x) + odds(y_l)) )

Intuitively, this is the negative log-probability of (the odds of good response) / (odds of good response + odds of bad response ).
If you minimize the average loss over multiple texts, it's the same as maximizing the odds that the model chooses winning response in every pair (of winning+losing responses).

6 videos in 7 days, I'm having a holiday and this is such a perfect-timing treat.

Thank you Mr Klicher for delving into the paper, ORPO; Monolithic Preference Optimization without Reference Model

Thanks for explaining basic terms along with the more complex stuff, for dilettantes like myself. Cheers.

The comparison in the end between OR and PR should also discuss the influence of the log sigmoid, or? And, more importantly, how the gradients for the winning and loosing output actually would look like with these simulated pars... It feels a bit handweavy why the logsigmoid of the OR should be the target ...

why hat, indeed

great! now apply ORPO to a reward model and round we go!

I feel like AI models have gotten more stale and same-y ever since RLHF became the norm. Playing around with GPT-3 was wild times. Hopefully alignment moves in a direction with more diverse ranges of responses in the future, and less censorship in domains where it's not needed.

Thank you for being awesome Yannic, I send people from the classes that I "TA" for to you because you're reliably strong with your analysis.

Would be interesting to see how it compares to KTO. Would guess that KTO outperforms and is easier to implament as you dont need pairs of inputs.

Nice I was waiting for this after you mentioned ORPO in ML News :))

I don't even know what the title of this video means 😵‍💫. But I'm going to watch anyway.

Great to see research from my homeland of South Korea represented!

You are on fire!

Nice!