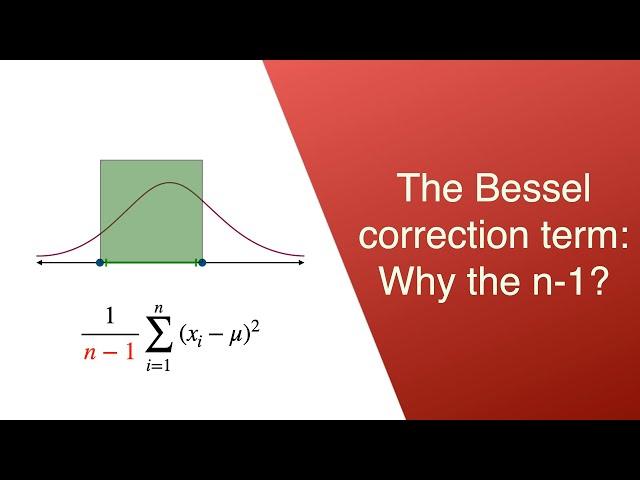
Why do we divide by n-1 to estimate the variance? A visual tour through Bessel correction

Correction: At 30:42 I write "X = Y". They're not equal, what I meant to say is "X and Y are identically distributed".

The variance is a measure of how spread out a distribution is. In order to estimate the variance, one takes a sample of n points from the distribution, and calculate the average square deviation from the mean.
However, this doesn't give a good estimate of the variance of the distribution. The best estimate, however, is obtained when dividing by n-1 instead of n.
WHY!?!?!?!?!?!?!?
In this video, we dig deeper into why the variance calculation should be divided by n-1 instead of by n. For this, we use an alternate definition of the variance, which doesn't use the mean in its calculation.

*[0:00] Introduction and Bessel's Correction*
- Introducing Bessel's Correction and why we divide by \( n-1 \) instead of \( n \) to estimate variance.

*[0:12] Introduction to Variance Calculation*
- Explaining the premise of calculating variance and introducing the concept of estimating variance using a sample instead of the entire population.

*[1:01] Definition of Variance*
- Defining variance as a measure of how much values deviate from the mean and outlining the basic steps of variance calculation.

*[1:52] Introduction to Bessel's Correction*
- Discussing why we divide by \( n-1 \) when calculating variance and introducing Bessel's Correction.

*[2:35] Challenges of Bessel's Correction*
- Sharing personal challenges in understanding the rationale behind Bessel's Correction and discussing my research process on the topic.

*[3:20] Alternative Definition of Variance*
- Presenting an alternative definition of variance to aid in understanding Bessel's Correction and expressing curiosity about its presence in the literature.

*[4:45] Quick Recap of Mean and Variance*
- Briefly revisiting the concepts of mean and variance, demonstrating how they are calculated with examples, and explaining how variance reflects different distributions.

*[7:05] Sample Mean and Variance Estimation*
- Explaining the challenges of estimating the mean and variance of a distribution using a sample and discussing why sample variance is not a good estimate.

*[8:49] Bessel's Correction and Why \( n-1 \) is Used*
- Explaining how Bessel's Correction provides a better estimate of variance and why we divide by \( n-1 \) instead of \( n \). Emphasizing the importance of making a correct variance estimate.

*[10:51] Why Better Estimation Matters?*
- Discussing why the original estimate is poor and why making a better estimate is crucial. Explaining the significance of sample mean as a good estimate.

*[13:02] Issues with Variance Estimation*
- Illustrating the problems with variance estimation and demonstrating with examples why using the correct mean is essential for accurate estimates. Explaining the accuracy of estimates made using \( n-1 \).

*[15:04] Introduction to Correcting the Estimate*
- Discussing the underestimated variance and the need for correction in estimation.

*[15:57] Adjusting the Variance Formula*
- Explaining the adjustment in the variance formula by changing the denominator from \( n \) to \( n - 1 \).

*[16:22] Calculation Illustration*
- Demonstrating the calculation process of variance with the adjusted formula using examples.

*[16:57] Better Estimate with Bessel's Correction*
- Discussing how the corrected estimate provides a more accurate variance estimation.

*[18:24] New Method for Variance Calculation*
- Introducing a new method for calculating variance without explicitly calculating the mean.

*[20:06] Understanding the Relation between Variance and Variance*
- Explaining the relationship between variance and variance, and how they are related mathematically.

*[21:52] Demonstrating a Bad Calculation*
- Illustrating a flawed method for calculating variance and explaining the need for correction.

*[23:37] The Role of Bessel's Correction*
- Explaining why removing unnecessary zeros in variance calculation leads to better estimates, equivalent to Bessel's Correction.

*[25:08] Summary of Estimation Methods*
- Summarizing the difference between the flawed and corrected estimation methods for variance.

*[26:02] Importance of Bessel's Correction*
- Emphasizing the significance of Bessel's Correction for accurate variance estimation, especially with smaller sample sizes.

*[30:19] Mathematical Proof of Variance Relationship*
- Providing two proofs of the relationship between variance and variance, highlighting their equivalence.

*[35:24] Acknowledgments and Conclusion*

Thanks @mkan543 for the summary!

Скачать видео