Комментарии:
Containerization with Docker and Kubernetes
TechBeyondAI
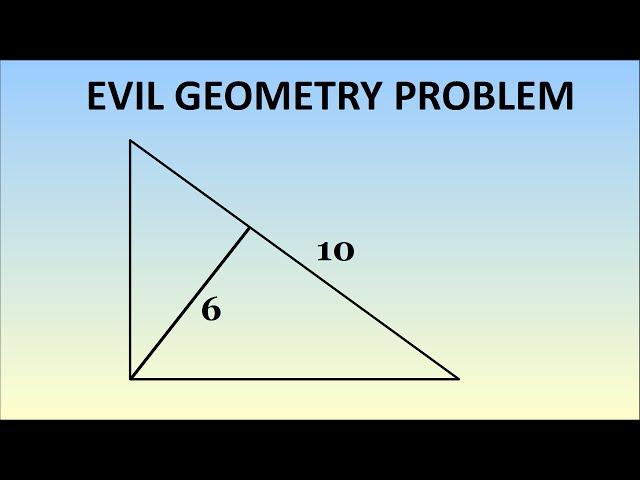
Evil Geometry Problem
MindYourDecisions
الدرس الاول ورشة اسكتش اب 2023 وفيراى 6 ( ريسبشن ) + Sketchup 2023 and Vray 6 Workshop
Amr Ashraf Innovations
Кулагины : 46-50 серии подряд
Детективные Сериалы
الدرس الاول ورشة اسكتش اب 2024 وفيراى 6 ( غرفة نوم ) - Sketchup 2024 and Vray 6 Workshop
Amr Ashraf Innovations
ЗАМОЧИТЕ ноги в УКСУСЕ и все БОЛЕЗНИ уйдут
Elena Matveeva
1. How Music Works - Acoustics for Musicians
Walk That Bass



![[Free] Pierre Bourne x Playboi Carti type beat "Indigo" (Prod.Fuckunixn) [Free] Pierre Bourne x Playboi Carti type beat "Indigo" (Prod.Fuckunixn)](https://invideo.cc/img/upload/QWQ1ZGZxSGNhLVo.jpg)




















