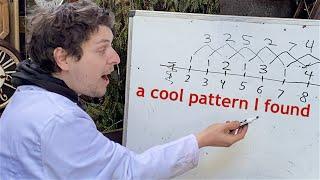
Fun Patterns I Found With Proper Divisors of Numbers

One pattern/rule about squares that i realized, x^2 = (x - 1)^2 + 2(x - 1) + 1. ex. 5^2 = 25, and 25 = 4^2 + (4 x 2) + 1, or 16 + 8 + 1. This works for any positive integer. you could also think of it as (and this is how i thought of this pattern/rule), 16 (the square of 4), is 9 away from 25. 4 times 2 = 8, and 8 + 1 = 9. to find the square value after 25, you add 11 (5 x 2 + 1), which is 36 (6^2). and 36 + 13 (6 x 2 + 1) = 49 (7^2), + 15 = 64, + 17 = 81, + 19 = 100, 121, 144, etc.

This is a nice technique to find some pythagorean triples. 25 = 16 + 9 = 5^2 = 4^2 + 3^2, therefore 5, 4, and 3 are pythagorean triplets. also 169 = 25 + 144 = 13^2 = 5^2 + 12^2. therefore 13, 5, and 12 are pythagorean triples. you can find any pythagorean triple set using this logic where the pythagorean triple sum (hypotenuse of the triangle) has a pythagorean triple additive (leg of the triangle) that is one less than the pythagorean triple sum(hypotenuse of the triangle), ex. 5 and 4 of the set 5, 4, and 3. 13 and 12 of the set 13, 12, and 5.

if 4 only has 2 factors, wouldn't 9 only have 2 factors? 1,3

taking the highest proper divisor of the odd numbers from 3 onwards, we get the following:
1, 1, 1, 3, 1, 1, 5, 1, 1, 7, 1, 5, 9, 1, 1, 11, ...

taking the sums of consecutive terms, we get the following:
2, 2, 4, 4, 2, 6, 6, 2, 8, 8, 6, 14, 10, 2, 12, ...

you may notice that every set of three terms forms a sum: that is, of the form a + b = c
however, if we go to 33, 35, 37 and 39 in the first sequence and the corresponding sums, we get the following:

11, 7, 1, 13
18, 8, 14

which does most certainly not form a sum. but why?
let's generalize.

call every set of four terms in the first sequence (starting from a multiple of 3, of course, to create the sums in the second sequence) a "chunk" - more specifically, we can notate a general "nth chunk" as the following (centered around 6n):
6n-3 6n-1 6n+1 6n+3

we can say for certain that, because each of the boundary terms (6n-3 and 6n+3) is a multiple of 3, that their highest proper divisors will be the corresponding factor (2n-1 and 2n+1 respectively), since the factor corresponding to 1 would be the number itself, of course, and therefore not a proper divisor. 6n-1 and 6n+1 are more tricky matters, however - so we'll call their highest proper divisors a and b respectively. notating this underneath the generalized chunk format, we get the following:

6n-3 6n-1 6n+1 6n-3
2n-1 a b 2n+1

the sums of consecutive terms, then, are as follows:

(2n - 1 + a), (a + b), (b + 2n + 1)

let's call a particular chunk "sum-compatible" if the sum condition we've established is true for that chunk.
we can write the sum condition as follows:

2n - 1 + a + a + b = b + 2n + 1

subtracting 2n and b from both sides, with a little rearranging:

a + a - 1 = 1
2a - 1 = 1

adding 1 and dividing by two, we see that, for a chunk to be sum-compatible, that a must be equal to 1.
but remember - a stands for the highest proper divisor of 6n-1. if this value is 1, then the only factors of 6n-1 would have to be 1 and 6n-1 - meaning that 6n-1 must be prime.

so, to summarize - we've established that, for the sums of consecutive highest proper divisors of odd numbers between 6n-3 and 6n+3 to themselves form a sum, that 6n-1 must be prime.

neat!

Similar to your equation to solve for number that give themselves if instead of taking the direct neighbors you increase the distance to an even number the even numbers will show themself. For example if you start at 6 2 spaces before 6 the GCD of 4 is 2 and 2 spaces after 6 the GCD of 8 is 4 added together becomes 6 again

Since 2 is the smallest possible divisor in every even number, the largest number you can divide it by is and always will be half of the even number. After all a bigger number would require a second factor to be smaller than the smallest divisor making it impossible to stay integer. Since an even number before a is just a-1 and an even number after a is just a+1, adding both halves together just gives you the average of the two neighbouring numbers, which will by definition lead to the number that's exactly in between it.

(a+1 + a-1)/2 = 2a/2 = a.

Maybe I was paying attention enough but aren't one, two, and 3 proper divisors of six and neighbors to one another? 1+2+3=6

Non-even threevens will have one third the number as their largest proper divisor. In fact, thinking about this more, the largest proper divisor of any composite number will be that number divided by the smallest prime factor. For example, 1729 is 7*13*19, so its largest proper divisor will be 13*19, which is 247.

How to be proficient in mental calculations ❓️

Your such a nerd. I love it

Love the abacus!! Great vid

Bro, it has to either be you or my old teacher, Mr Cooper. Who shot me in the stomach with a 22 pistol in my dream the other night. Had to be, whyd you do it, bro, I'm gonna die now, probably

Goated channel and goated content

you got back to interesting. good...

For odd numbers k, the count of odd numbers less than k is equal to (k-1)/2, i.e., the greatest proper divisor of the even number one less than k.

Huh, that is cool! All the patterns I saw looking at that look more like Law of Small Numbers patterns, unfortunately.

Very fun!

Thanks for the fun video, Domotro.

If we define factors F of a number N as any number which can multiply N with 1/F, where neither F nor N* 1/F is a fraction then
The factors of 1 is -1, 1, i and -i

Pi is encoded between 6 - 8, whose center number is a 7.
The largest factors being....3 • 1 • 4

If we draw a triangle here connecting the base numbers........... 6, 7 & 8 and the one above the 7 for its largest factor, making a triangle of the 3 base integers and the factor 1 above 7, we get 22.

Now we can either beget a 7 from the largest factors of 6 and 8, being 3 and 4 and add them to get our 7 or we can get the actual 7 linked above them. Either way if we consider the triangle to be a body or field, that 7 is running straight up and down through the middle of the body or field. Which, if we pay our due diligence to PI as a diameter running through the center of a circle, the 7 here is doing the same with this holographic, incorporeal triangle.

22 ÷ 7 = π ~~ or close enough it makes no matter.

And from what we know, Heaven or the circle is represented by the number 3. And Earth, a square, number 4.

And what is floating above this triangle to the left and right? A 3 & 4. Or the 7 at the apex of the triangle, and the 7 beaming in a straight line up from the top vertex.

Also, if we lay out a regular number line up to at least 15, we find Pi upon it.

@ 13 • 14 • 15.....there it is.

1 as the diameter giving us the remaining numbers of...3 1 4 1 5

Add these up and we get 42, which is not only the apex degree of a primary rainbow, which makes Pi with the ground but this is also encoded in the 42 generations from Adam to Christ in Matthew 01.

Adam to David = 14 Generations
David to Babylon = 14 Generations
Babylon to Christ = 14 Generations

3 × 14 = 42......and it is 3 = 14's

Hence Matthew= Math You

The diameter is male and circumference female and these 2 together give us the endless stream of digits producing creation, where the piper pipes forth an endless stream of numbers, music and a uni-verse.....one song.

SONG = SON-G

The capital letter A is the Road of the Golden Path.
Adam is an Atom

Jesus = G-Suss

And in Septenary Gematria, the word SIX is 653, giving us 14.
So 666 or SixSixSix = 42, or 3-14's.

666 = a cube of 6×6×6 = 216
Which is a decimated fractal of 2,160 which is the degrees of the Net of the Cube.

And SEVEN in Septenary Gematria = 22
22 ÷ 7 = π

And also there are 5 letters, and the square root of 5 = 2.2, a decimated fractal of 22.

I feel like you’re gonna make this your main channel

Yeah

If you play the same game and add the neighbours of the top row of numbers then you always get an even number and if you add 2 consecutive terms from that row you get an odd number - also kinda obvious but kinda cool, lol

We can always count on Carlo 😎