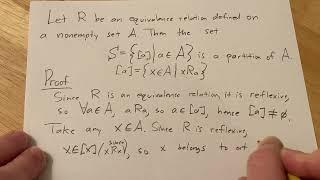Important Math Proof: The Set of Equivalence Classes Partition a Set

Very nice explanation!

Thank you so much for your detailed explanation! I have finally understood it.

Thank you so very much for explaining this. Your video most certainly helped me to understand this better.

so where is antisymmetric?

We don't need to prove that all the elements in equivalence relation set form the whole set A?

chill vids. thanks for the uploads (=

That's a really good way of looking at the Partition Problem. A lot of solutions rely on brute force, dynamic programming, etc. and in this case you have a way to do this declaratively by inspecting each element of the set. Heck, if you know a little bit about the problem in advance, you can even specify the equivalence classes, making the partition operation more computationally feasible.

Props for approaching a subject that is beyond the normal exposure to mathematics of a tipical highschool or even college graduate! And good choice of subect in terms of difficulty.

In case you want some unsolicited advise: you mentioned this result is cool, but didn't really give a example of something cool you can do with it. It would be nice to have an example of the result being used

lol why is it in my recommended? I am asian, yes, but not THIS much

I wanted to explicitly show that x belonged to a unique equivalence class using the definition of unique existence, just because of the idea of a widespread trend of computers checking proofs, which might get popular in the near future. We want to show that Forall x, Exists, or in other words, that there's a unique equivalence class [y] of x. The definition of unique existence is that there exists an element m such that P(m), and that if any other element n is such that P(n), then m=n.

We let x be an arbitrary element of A. We showed x in [x]. Then we let [b] be an arbitrary equivalence class that is a subset of A. We showed that if x in [b], that [x]=[b]. (You used [a] instead of [x], but of course, your logic shows just the same that if x in [x] and x in [b], then [x]=[b]). Since [b] was arbitrary, it is the case that (changing the dummy variable from [b] to [z]) Forall [z], x in [z] implies [x]=[z]. Combining statements, we have that x in [x] AND Forall [z], x in [z] implies [x]=[z].

I'm not to sure on how the scope of quantifiers works if I want to do an existential generalization on [x], but I believe it would go like this seeing as how [x] is free in the "Forall [z], x in [z] implies [x]=[z]" statement:

Exists[y](x in [y] AND Forall [z], x in [z] implies [y]=[z]).

Then since x is arbitrary, we had a universal derivation of the statement Forall x, Exists[y](x in [y] AND Forall z, x in [z] implies [y]=[z]).
In more abstract writing, just focusing on the existence part of the statement, that would say Exists Y (P(Y) AND Forall Z (P(Z) implies Y=Z).

I think that checks out?

Transitivity is more obvious for me as a b c are elements of A then if aRb and bRc then aRc and see if it satisfies

For symmetry we can say if xRa then aRx and see if it satisfies.

R is a subset of AxA?