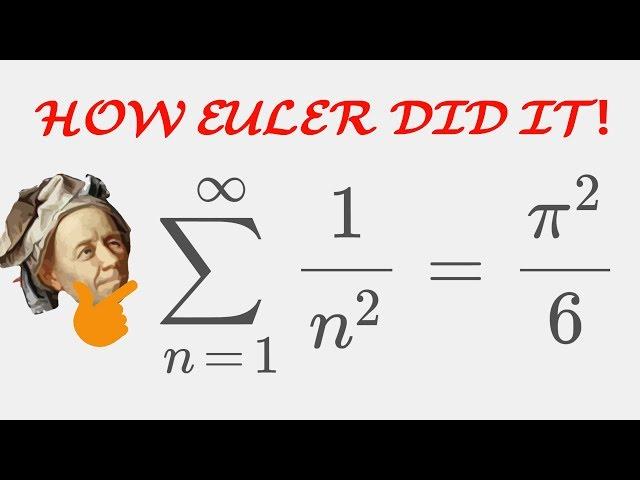
But HOW did Euler do it?! A BEAUTIFUL Solution to the FAMOUS Basel Problem!
Комментарии:
Navya ko kaise chot lag gayi #unbelievablenavya #shorts #funny #navya
Unbelievable Navya
Clozapine Success With Schizophrenia | My Journey with Treatment-Resistant Schizophrenia
Surviving Schizophrenia
EMA Dental Porcelain Veneer Procedure (2018)
EMA Dental & Refresh
Нельзя смеяться | Смех с водой | 97 #shorts
Коммент.Шоу
Neverwinter - Power Sets Guide
Garlaanx